이진탐색 | JavaScript

October 16, 2023

Algorithm이진탐색

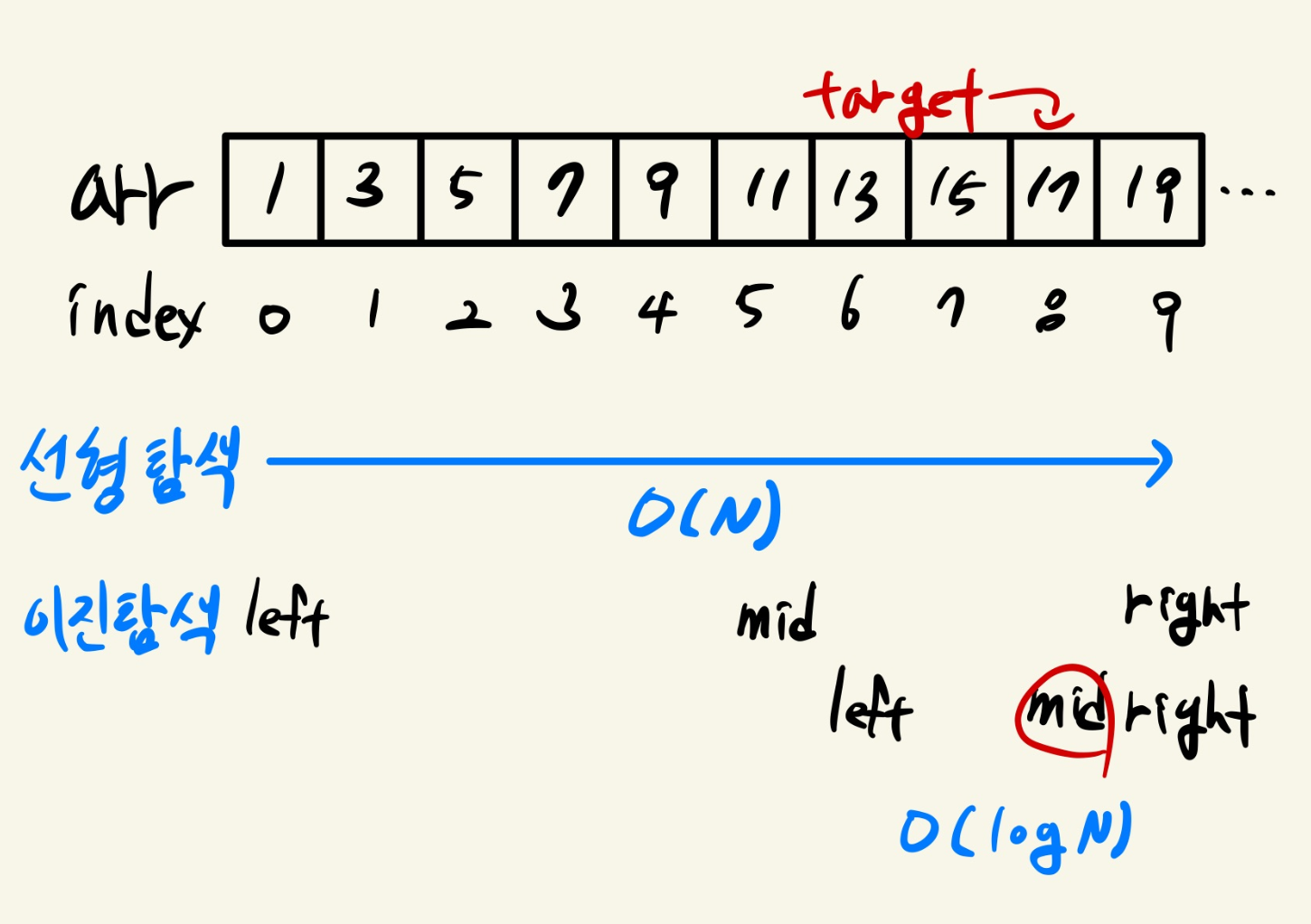
배열 [1, 3, 5, 7, 9, 11, 13, 15, 17, 19]에서 17의 인덱스 값을 찾는다고 해봅시다. 직관적인 생각은 앞에서부터 순차적으로 값을 찾아 확인해보는 선형탐색을 떠올릴 수 있습니다. 하지만, 주어진 배열처럼 길이가 작은 배열이 아니라 길이가 큰 배열이라면, 인덱스 값을 찾기 위해 오랜 시간이 걸릴 수도 있습니다.

어떻게 하면 더 빠르게 원하는 인덱스 값을 찾을 수 있을까요?

만약 배열이 정렬되어 있다면, 배열의 중간값을 고르고, 중간값과 찾는값을 비교하여 찾는 시간을 줄일 수 있습니다. 이러한 알고리즘을 이진탐색 알고리즘이라고 부릅니다.

이진탐색을 사용하기에 적합한 경우는 다음과 같습니다.

매우 넓은 범위를 다루는 경우
데이터를 정렬한 뒤 다수의 쿼리를 날려야하는 경우

이진탐색 구현

이진탐색을 구현하기 위한 두 가지의 방법이 있습니다.

다시 말하지만, 이진탐색을 하기 위해선 배열이 정렬되어 있어야 합니다.

1. 재귀함수로 구현하기

function binarySeach(arr, target, start, end) {
  // 탈출조건: 값을 찾지 못하는 경우
  if (start > end) return -1;
 
  // 중간값을 계산한다.
  let mid = parseInt((start + end) / 2);
 
  // 찾는 값과 중간값이 일치한다면 그 인덱스를 반환한다.
  if (arr[mid] === target) return mid;
  // 찾는 값보다 중간값이 더 크다면, 끝 범위를 좁혀준다.
  else if (arr[mid] > target) return binarySeach(arr, target, start, mid - 1);
  // 찾는 값보다 중간값이 더 작다면, 시작 범위를 좁혀준다.
  else return binarySeach(arr, target, mid + 1, end);
}
 
const target = 17;
const arr = [1, 3, 5, 7, 9, 11, 13, 15, 17, 19];
 
console.log(binarySeach(arr, target, 0, arr.length - 1)); // 8

2. 반복문으로 구현하기

function binarySearch(arr, target, start, end) {
  while (start <= end) {
    let mid = parseInt((start, end) / 2);
 
    if (arr[mid] === target) return mid;
    else if (arr[mid] > target) end = mid - 1;
    else start = mid + 1;
  }
  return -1;
}
 
const target = 17;
const arr = [1, 3, 5, 7, 9, 11, 13, 15, 17, 19];
 
console.log(binarySeach(arr, target, 0, arr.length - 1)); // 8

이진탐색 활용

1. 정렬된 배열에서 특정 원소의 개수 구하기

숫자 카드 2 문제를 이전에 Set을 이용해서 풀었었는데 이진탐색을 이용해서 풀 수도 있습니다.

문제를 요약하면 N개의 카드를 가진 카드배열이 하나 주어지고, M개의 카드를 가진 카드배열이 하나 더 주어집니다. M개의 카드를 가진 카드 배열에서 카드를 하나씩 뽑아 뽑은 숫자가 N개의 카드배열에 몇개 있는지 하나씩 출력하는 문제입니다.

N, M의 범위는 최대 500,000으로 이중 for문으로 문제를 풀면(O(N^2)), 시간 초과가 나오기 때문에 이진탐색을 활용하여 문제를 해결할 수 있습니다.

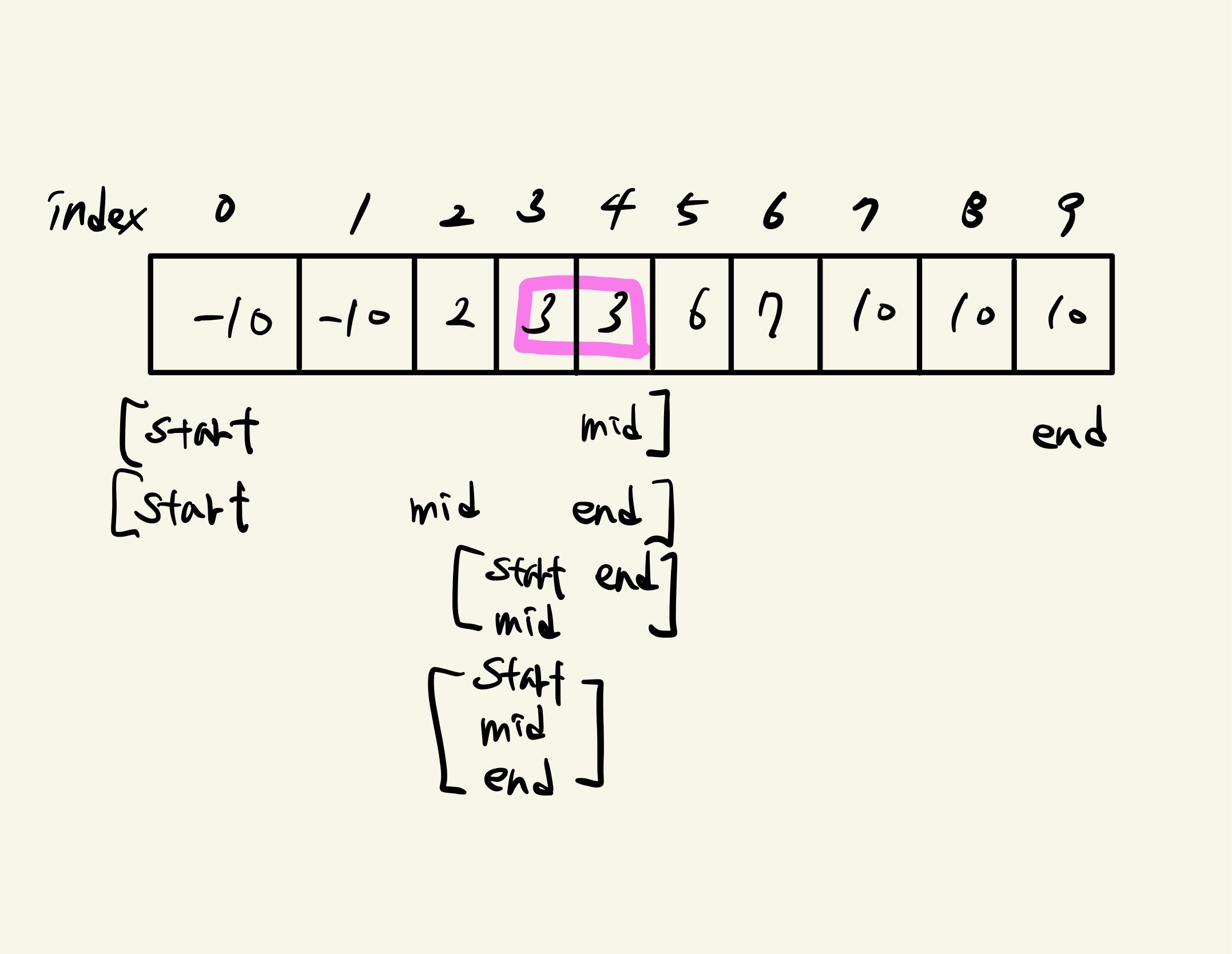
하한선을 구하는 함수

function lowerBound(arr, target, start, end) {
  while (start < end) {
    let mid = parseInt((start + end) / 2);
    // 값을 찾았더라도, 왼쪽으로 값을 계속 밀어준다. 
    // 값이 하나 있을 경우, 현재 값도 포함해야하기 때문에 mid - 1이 아니라 mid를 넣어준다.
    if (arr[mid] >= target) end = mid;
    else start = mid + 1;
  }
  return end;
}

상한선을 구하는 함수

function upperBound(arr, target, start, end) {
  while (start < end) {
    let mid = parseInt((start + end) / 2);
    // 찾고자하는 값보다 큰 값 중에서 가장 왼쪽 위치를 찾는다.
    if (arr[mid] > target) end = mid;
    else start = mid + 1; // 최대한 오른쪽으로 이동하기
  }
  return end;
}

하한선, 상한선을 이용해 숫자를 세는 함수

function countByRange(arr, leftValue, rightValue) {
  const leftIndex = lowerBound(arr, leftValue, 0, arr.length);
  const rightIndex = upperBound(arr, rightValue, 0, arr.length);
  return rightIndex - leftIndex;
}

풀이

const fs = require('fs');
const input = fs.readFileSync('/dev/stdin').toString().split('\n');
 
// 이분탐색으로 풀기
const N = Number(input[0]);
const cards1 = input[1].split(' ').map(Number);
const M = Number(input[2]);
const cards2 = input[3].split(' ').map(Number);
 
cards1.sort((a, b) => a - b);
 
let answer = '';
for (let i = 0; i < cards2.length; i++) {
  const card = cards2[i];
  const count = countByRange(cards1, card, card);
  answer += count + ' ';
}
console.log(answer);

이분탐색을 활용하면 O(N * logN)의 시간복잡도로 문제를 해결할 수 있습니다.